Logični operatorji (logična vrata)
Kaj se bomo v tem poglavju naučili
Spoznali
bomo logična vrata ter njihovo uporabo za realizacijo logičnih funkcij,
aritmetičnih operacij in pomnilniških celic.
Logična vrata
Logična vrata so preprosto digitalno elektronsko vezje, ki opravlja določeno logično funkcijo:
|
Logična vrata so element, ki logičnim stanjem na vhodnih
sponkah priredi ustrezno logično stanje na izhodni sponki. |
|
|
Z uporabo logičnih vrat gradimo vezja kombinacijske logike, vezja za izvajanje
aritmetičnih operacij, pomnilniška vezja ...
Osnovne logične funkcije vrat so naslednje:
- negacija (NE, angl. NOT),
- konjunkcija (IN, angl. AND) in
- disjunkcija (ALI, angl.OR), pogosto pa se uporabljajo še nekatere druge vrste vrat:
- izključujoči ALI (XOR)
- NE-IN (NAND),
- NE-ALI (NOR) ter
- NE (negator, angl. NOT), ki so "vrata" z enim vhodom.
Podrobneje so opisane v nadaljevanju.
Primer:
Trivhodna vrata IN (angl. AND) dajo na izhodnem priključku visoko
stanje, če je na vseh treh vhodnih sponkah visoko stanje: na prvi IN
drugi IN tretji vhodni sponki.
Besedni opis predstavimo bolj skrčeno z logično funkcijo in logičnim vezjem.
- Logično funkcijo za opisano zvezo zapišemo takole: Y = A IND B IN C
- Grafično pa jo prikažemo z ustreznim simbolom za vrata IN:
Učinek posameznih vrat je opisan v spodnji tabeli. Za vsaka logična vrata
sta narisana evropski (IEC) simbol in - iz praktičnih razlogov - še ameriški.
simbol. Sledi opis in pravilnostna tabela, ki za vsako stanje na vhodu
prikazuje rezultat na izhodu vrat. Iz pravilnostne tabele lahko
ugotovimo, pri katerih vhodnih stanjih dobimo na izhodu logično 1.
|
ime vrat |
IEC simbol vrat |
ameriški simbol |
opis |
pravilnostna tabela |
||||||||||||||||||
|
IN, |
|
|
Y = A AND B |
|
||||||||||||||||||
|
ALI, |
|
|
Y = A OR A |
|
||||||||||||||||||
|
NE, |
|
|
Y = NOT A (ali: Y = / A) |
|
||||||||||||||||||
|
izključujoči ALI, |
|
|
Y = A XOR B |
|
||||||||||||||||||
|
NE-IN, |
|
|
Y = NOT ( A AND B) |
|
||||||||||||||||||
|
NE-ALI, |
|
|
Y = NOT ( A OR B) |
|
||||||||||||||||||
Interaktivni primer
Nastavimo dvojiški vhod in opazujmo izhode iz vrat:
Zanimivost!
Iz samih negiranih-IN vrat (NE-IN oz.NAND) lahko sestavimo vse
ostale logične funkcije! Isto velja tudi za negirana vrata ALI (NOR).
Logična vrata so po zgradbi preprosta vezja - iz nekaj tranzistorjev. Prva
vrata so bila iz bipolarnih tranzistorjev, danes so aktualna vrata iz MOS
tranzistorjev.
Poglejmo, kaj vse je možno zgraditi z uporabo vrat!
1. Logična vezja
Izhode logičnih vrat lahko povežemo na vhode drugih logičnih vrat in tako
gradimo bolj kompleksna logična vezja. Najbolj značilna so
- kombinacijska logična vezja,
- kodirniki, dekodirniki,
- multiplekserji, demultiplekserji,
- generator parnostnega bita,
- in druga.
Logična vrata dobimo "pakirana" v integriranih vezjih različnih
tehnologij (TTL, CMOS ...). Podrobnosti o posameznem vezju poiščemo v
dokumentaciji (angl. datasheet) pri proizvajalcu. Pri vgradnji takšnih
vrat moramo upoštevati električne značilnosti vezja, funkcijo vgrajenih
vezij in pomen priključkov. Na sliki je prikazan razpored priključkov v
integriranem vezju s štirimi vrati vrste NE-IN (angl. NAND), simboli so
ameriški.
Slika: Funkcionalna zgradba in razpored priključkov integriranega vezja z logičnimi vrati.
|
Slika: Primer kombinacijske logike: logično vezje, zgrajeno iz različnih logičnih vrat. Funkcionalno je to vezje, pri katerem s kombinacijo izbirnih signalov A izberemo enega od izhodnih signalov Oi, ki bo dajal nizko stanje (ostali pa visoko). Prikazano vezje je realizirani v obliki integriranega vezja. Tudi sicer je realizacija neposredno z vrati danes redka - obstajajo bolj ekonomični načini, na primer s programirljivo logiko. |
Poglejmo še en preprost primer uporabe vrat: krmiljnje vrat.
S krmilnim signalom na vratih IN prepuščamo oziroma zadržujemo logično
stanje, ki je trenutno prisotno na drugem vhodu teh vrat.
Ko je krmilni signal v stanju 1, se stanje drugega vhodnega signala
prenese na izhod. Ko je krmilni signal v stanju 0, je na izhodu
stanje 0, ne glede na stanje drugega vhodnega signala.
|
|
|
Slika - levo:
Uporaba logičnih vrat IN za - vrata! Ko ima krmilni signal vrednost 1, se
stanje iz vhoda prenaša na izhod.
Ko ima krmilni signal vrednost 0, je tudi na
izhodu signal nič - vrata so "zaprta"!
Slika - desno: časovni diagram prikazanih signalov.
2. Aritmetična vezja
Z logičnimi vrati lahko gradimo tudi vezja, ki izvajajo aritmetične
operacije: seštevanje, odštevanje… Za zgled omenimo binarni seštevalnik.
Gre za relativno preprosto vezje, s katerim realiziramo aritmetično operacijo
seštevanja dveh (dvojiško predstavljenih) števil. Skratka, prava
aritmetična operacija, seštevanje.
Spomnimo se, da se osrednji del mikroprocesorja imenuje aritmetično-logična
enota.
Začni s polovičnim seštevalnikom: pri seštevanju dveh enobitnih vrednosti
"izračuna" vsoto in morebitni prenos.
Slika: Enobitni polovični seštevalnik v izvedbi z logičnimi vrati.
Polovični seštevalnik nadgradimo v polni enobitni seštevalnik, kjer poleg enobitnih števil upoštevamo še morebitni prenos.
Slika: Naslednji korak je enobitni polni seštevalnik: poleg dveh bitov števila upošteva še morebitni prenos c (angl. carry):
Sestava osmih polnih enobitnih seštevalnikov "zmore"
seštevanje dveh osembitnih števil. Upošteva vse vmesne prenose. Polni
osembitnbi seštevalnik ima - čeprav je narejen kot logično vezje - aritmetično
funkcijo. Z majhnimi dopolnitvami ga nadgradimo v odštevalnik. Kot tak
predstavlja osnovo za aritmetično računsko enoto v mikroprocesorju.
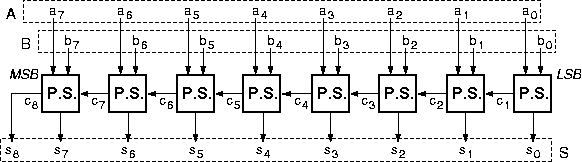
Slika: Polni
8-bitni seštevalnik. 8-bitni števili A in B se seštejeta z osmimi polnimi
seštevalniki (P.S.).
Rezultat je 8-bitna vsota S in morebitni
prenos s8 , na najte�jem mestu.
Seštevalno vezje opravlja aritmetično operacijo seštevanja dveh 8-bitnih števil, upoštevaje morebitni prenos.
Interaktivni primer:3. Pomnilniška vezja
Pomembna vezje, zgrajeno iz logičnih vrat, je pomnilniška celica (tudi flip-flop),
ki ima dve stabilni stanji, med katerima jo lahko preklapljamo z
zunanjim krmilnim signalom. Vsiljeno stanje lahko ohrani, dokler ima
napajanje, in je kot taka že prava pomnilna celica. Takšne celice
gradimo v registre različnih vrst - pomnilniške, pomikalne registre, pa tudi
binarne števce, sekvenčna vezja.
Na sliki je prikazana pomnilniška celica, prirejena za uporabo kot pomnilnik.
Informacija, ki jo hrani, je velika 1 bit.
|
Slika: Zgraba celice D iz logičnih vrat. Takšno vezje prenese vrednost iz vhoda D na izhod Q, če je na vhodu CLK visoko stanje oz. ob impulzu. Pomen preostalih priključkov: Q' je invertirani izhod; z vhodoma PRESET in CLEAR pa vsilimo stanje 1 oziroma 0. |
Slika: Simbol za D celico s podatkovnim vhodom D, taktnim vhodom CLK, izhodom Q in invertiranim izhodom Q' ter nastavitvenima vhodoma za vpis in brisanje. |
Ko združimo več pomnilniških celic, na primer 8 ali 16, dobimo
register. Večje število urejenih registrov - tudi na tisoče, pa je pomnilnik.
4. Števci
Še en primer uporabe celic (zgrajenih iz logičnih vrat!) je
vezje števca. S prihajajočimi impulzi se stanje na izhodnih sponkah
spreminja. Vrstni red teh stanj je lahko naraščajoče dvojiško zaporeje, lahko
je padajoče, lahko je BCD ali kako drugače kodirano zaporedje - odvisno od
dodanih povezav. Z različnimi dodanimi povezavami dobimo številne
različice števnih vezij.
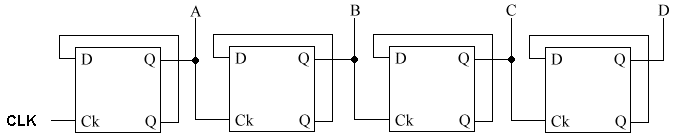
Na sliki je primer zgradbe 4-bitnega binarnega števca. Z uporabo
nastavitvenih vhodov PRESET in CLEAR bi lahko nastavili začetno
stanje števca ali ga v poljubnem trenutku izbrisali (postavili na vrednost
0000). Na sliki je torej preprosta različica števca.
|
Slika: S
štirimi celicami lahko zdradimo 4-bitni binarni števec: Ob impulzih na sponki
Ck (Clock, ura), |
POVZEMIMO!
Logična vrata so vmesni člen med tranzistorji kot najosnovnejšimi gradniki
digitalnih vezij in kompleksnejšimi digitalnimi vezji. Opravljajo določeno logično
funkcijo. V vezjih igrajo vlogo logičnih operatorjev. Z njmi gradimo
zahtevneše sklope. Najpomembnejše skupine so:
- Kombinacijska logična vezja so vezja, kjer so stanja na izhodnih priključkih po določeni logični funkciji odvisna od stanj na vhodnih sponkah.
- Aritmetična vezja so v svojem bistvu kombinacijska logična vezja, vendar je njihov učinek navzven enak določeni računaki operaciji.
- Pomnilniška celica je vezje, ki lahko določeno stanje električne napetosti ohrani. Skupina takšnih celic je register. Za pomnilnik potrebujemo veliko števil pomnilniških celic.
Vsa našteta področja so zastopana tudi v mikroprocesorju.
Naloge |
1. Iz vrat NAND "sestavi" negator! Nariši logično
vezje in s pravilnostno tabelo prikaži delovanje vezja.
|
2. Na sliki je narisano logično vezje, v katerem
so uporabljena vrata NE-IN (NAND), narisana z ameriškimi simboli. Z modro
barvo so vrisane povezave, ki smo jih naredili uporabniki. |
|