
Spoznali bomo nekaj tipičnih primerov zveznih veličin in kaj je njihova skupna značilnost. Spoznali bomo, kdaj uporabljamo digitalne podatke. Obravnavali bomo problem natančnosti digitalnih podatkov, kakršne uporabljamo tudi v digitalnih računalnikih.
V vsakdanjem življenju imamo pogosto opravka z zveznimi veličinami. To so na primer fizikalne veličine, ki lahko v določenem intervalu (včasih tudi neskončnem) zavzamejo poljubno vrednost. To je povsem analogno temu, da imamo na premici in celo na daljici neskončno število točk. Isto seveda velja za število točk na poljubni krivulji.

Vzemimo za primer merjenje temperature s klasičnim živosrebrnim termometrom. Ali merjenje hitrosti avtomobila s klasičnim merilnikom hitrosti s kazalcem. Tako temperatura kot hitrost lahko v predvidenem območju zavzameta poljubno vrednost. Iz prej omenjene analogije s točkami na krivulji pravimo, da so podatki o takih veličinah zvezni. Včasih jim pravimo tudi analogni.
Instrumenti, ki na ta način prikazujejo veličine, so analogni instrumenti. Kako natančno razberemo tako veličino, je odvisno od kvalitete instrumenta, pa tudi od našega občutka.

Danes se čedalje bolj uveljavljajo digitalne naprave, in to niso samo računalniki. Da bi te lahko uporabljale in prikazovale zvezne veličine iz resničnega sveta, morajo njihove signale najprej digitalizirati.
Že zaradi samega prikaza - kot bomo pa malo kasneje
spoznali
tudi zaradi notranjega pomnenja takih podatkov - pravimo, da imamo
sedaj
diskretne podatke.  Poglejmo
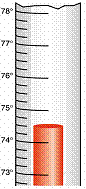
si na primer prikazani digitalni termometer. Ali lahko
prikaže vrednost 31.467 0C ? Seveda ne. Lahko prikaže
31.4 0C
ali 31.5 0C, ne pa vmesnih vrednosti. In tudi če bi imeli
termometer
z več številkami, bi si lahko zastavili podobno vprašanje. Ker torej
lahko
prikažemo le določene vrednosti, ne pa kakršnihkoli, so taki podatki
diskretni.
Poglejmo
si na primer prikazani digitalni termometer. Ali lahko
prikaže vrednost 31.467 0C ? Seveda ne. Lahko prikaže
31.4 0C
ali 31.5 0C, ne pa vmesnih vrednosti. In tudi če bi imeli
termometer
z več številkami, bi si lahko zastavili podobno vprašanje. Ker torej
lahko
prikažemo le določene vrednosti, ne pa kakršnihkoli, so taki podatki
diskretni.
In ta problem je prisoten v vseh digitalnih napravah, tudi v računalnikih.
Razlog je v tem, da posamezne podatke pomnijo z množico bitov. Ta je omejeno velika, čeprav je ta meja čedalje večja. V nekaterih primerih uporabljamo za vsak podatek po 8 bitov, drugič po 16 ali še več. Praviloma pa je to število mnogokratnik števila 2. Višje kot je, bolj natančno oziroma verodostojno lahko nek podatek pomnimo, uporabljamo oziroma prikazujemo. Pravimo, kako na drobno nek zvezni podatek kvantiziramo.
Na spodnjem interaktivnem primeru izberimo število bitov digitalnega registra in opazujmo kvantizacijo analognega območja. Izberimo posamezne primere analognih vrednosti in opazujmo, kakšni so njihovi digitalni ekvivalenti (pri izbranem številu bitov v registru):
|
|
Primer digitalizacije analognih vrednosti v območju med 0.0 in
256.0: |
8 bitna natančnost zagotavlja 256 nivojev, kar je verjetno dovolj za merjenje temperature. 16 bitna natančnost zagotavlja pa že kar 65536 nivojev. Spomnimo se, da smo se v računalnikih včasih zadovoljili z 8 bitnimi zvočnimi karticami, danes pa vemo, da je to za verodostojno pomnenje in reprodukcijo zvoka premalo.
Seveda velja vse to tudi za obdelavo podatkov z računalniki. Včasih smo poznali tudi analogne računalnike, danes pa le še digitalne. Pri sodobnih računalnikih je natančnost podatkov sicer lahko zelo velika, vendar kljub temu omejena. (Digitalni) računalniki ne zmorejo dela z analognimi podatki, zato moramo tudi analogne podatke prej digitalizirati.
Kot primer analognega podatka lahko gledamo tudi na barve oziroma na barvno lestvico, ki lahko v realnem svetu zavzame neskončno odtenkov, tudi če se omejimo le na vidni spekter barv.
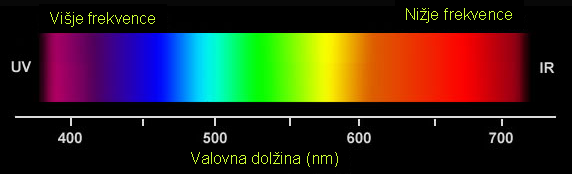
To pa ne velja za računalniško, digitalno predstavitev, kjer vsak piksel podajamo z omejenim številom bitov.
|
Na levem interaktivnem primeru izberi, s koliko biti (na posamezno RGB komponento) želiš podati barvo piksla na zaslonu računalnika. Število bitov na piksel je 3 krat večje. Opazuj, koliko različnih barvnih vrednosti imaš na voljo pri danem številu bitov na RGB komponento barve za vsak piksel |